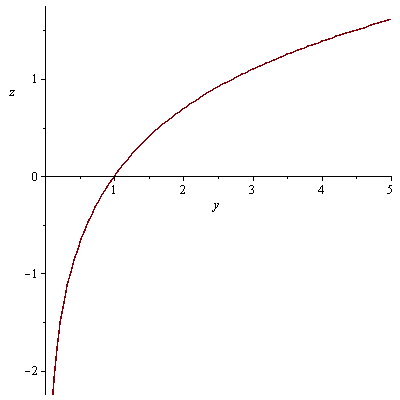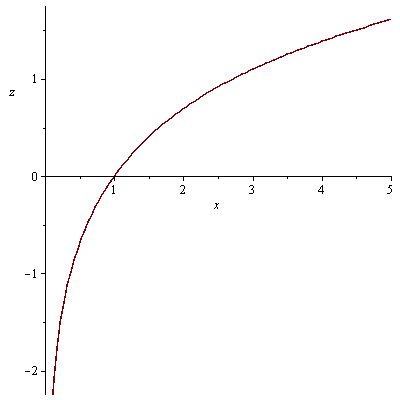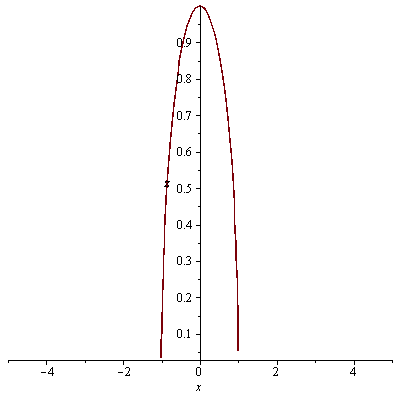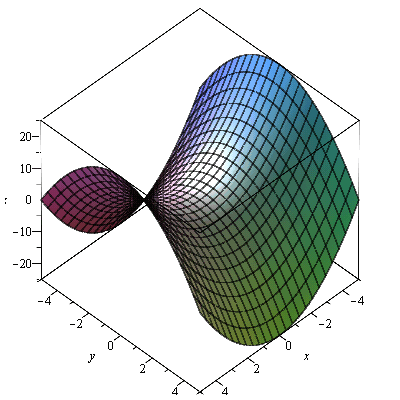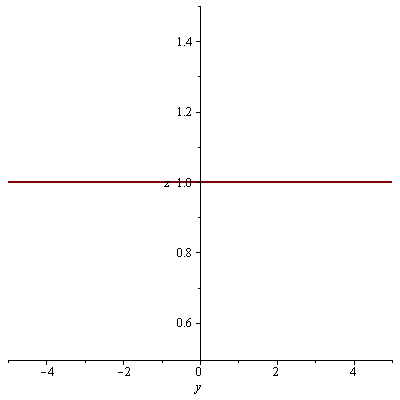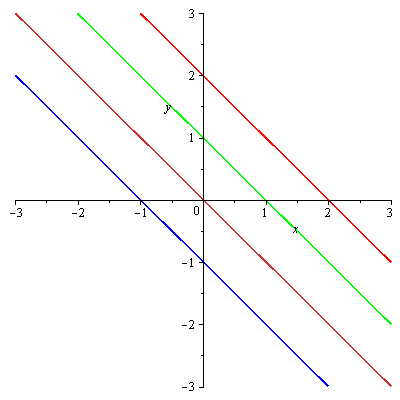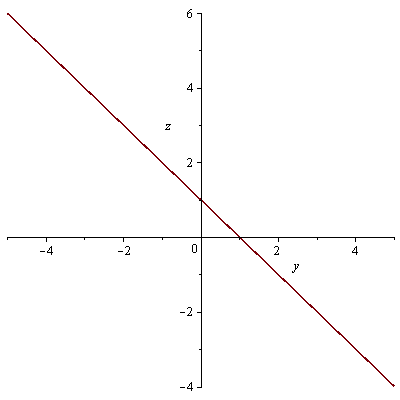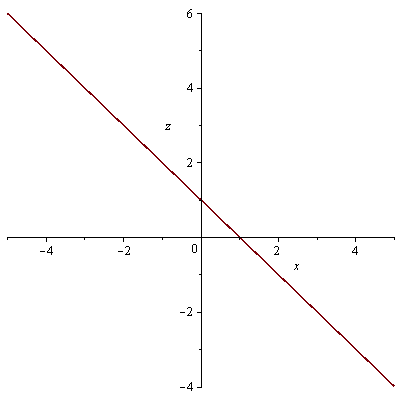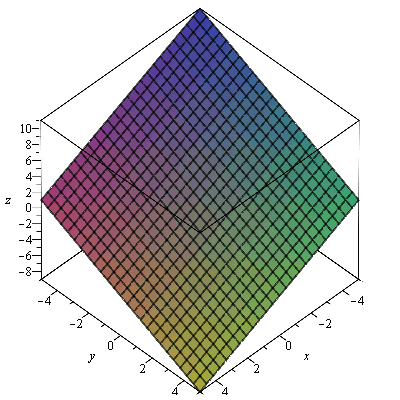ln(x+y) 

funkce 

>	f1:=(x,y)->ln(x+y);

 

(1.1)

 

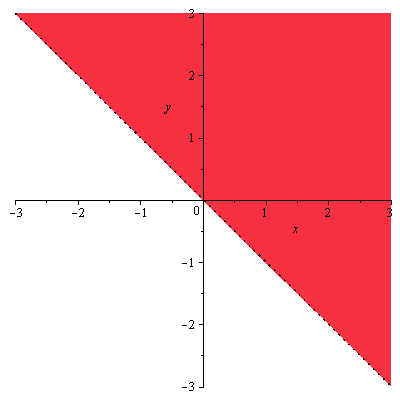
definiční obor 

>	implicitplot(x+y>0,x=-3..3,y=-3..3,filledregions=true);

 

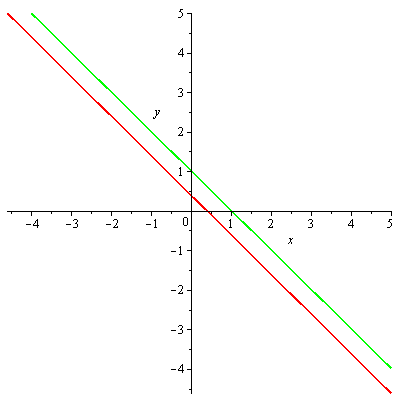
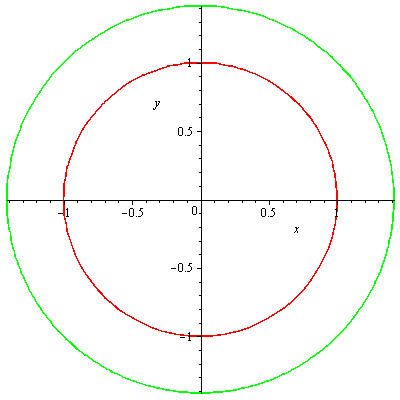
vrstevnice 

>	implicitplot([f1(x,y)=-1,f1(x,y)=0,f2(x,y)=1], x=-5..5, y=-5..5,gridrefine = 2, grid=[10,10], color=[red,green,blue]);

 

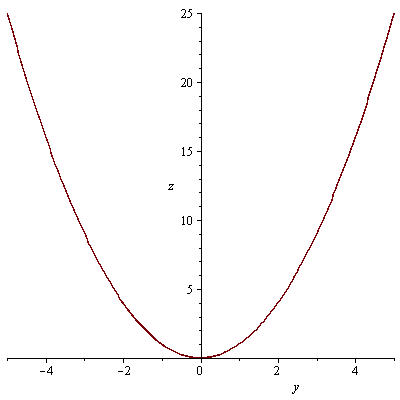
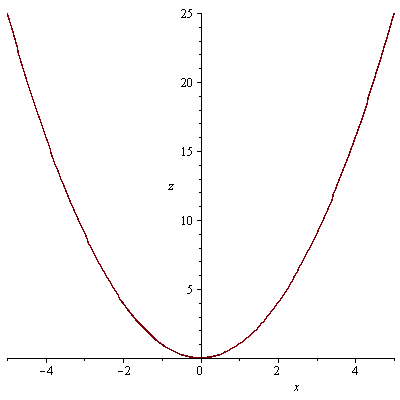
průsečnice s rovinami x=0 a y=0 

>	plot(f1(0,y),y=-5..5, labels=[y, z]); plot(f1(x,0),x=-5..5, labels=[x, z]);

 

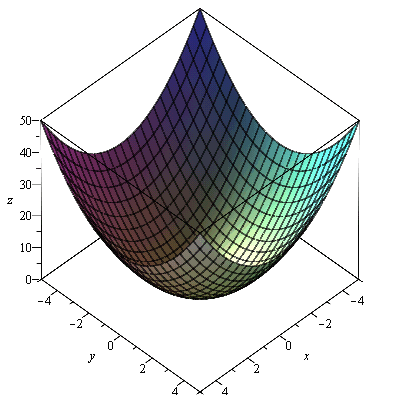
graf 

>	plot3d(f1, -5..5, -5..5, labels=[x, y, z]);

 

>

 

sqrt(1-x^2)+sqrt(y^2-1) 

funkce 

>	f2:=(x,y)->sqrt(1-x^2)+sqrt(y^2-1);

 

(2.1)

 

definiční obor 

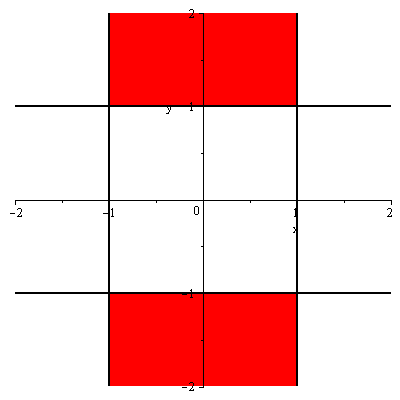
>	inequal( {1-x^2>=0,y^2-1>=0}, x=-2..2, y=-2..2, color=red);

 

vrstevnice 

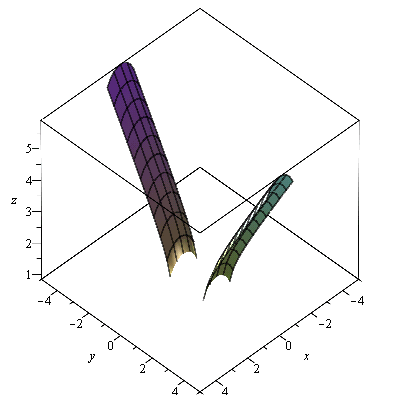
>	implicitplot([f2(x,y)=1,f2(x,y)=2], x=-1..1, y=-5..5,gridrefine = 2, color=[red,green]);

 

průsečnice s rovinami x=0 a y=0 

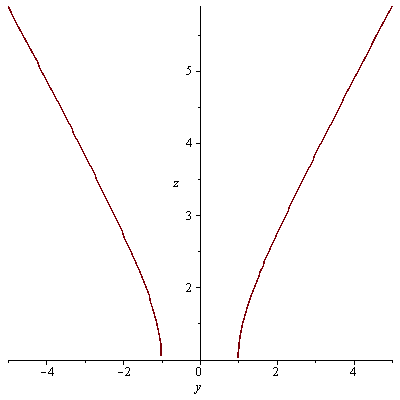
>	plot(f2(0,y),y=-5..5, labels=[y, z]); plot(f2(x,0),x=-5..5, labels=[x, z]);

 

 

 

Warning, unable to evaluate the function to numeric values in the region; complex values were detected

 

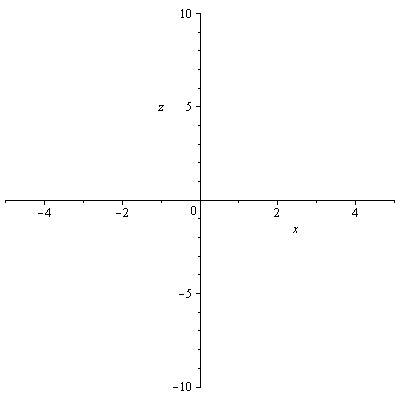graf 

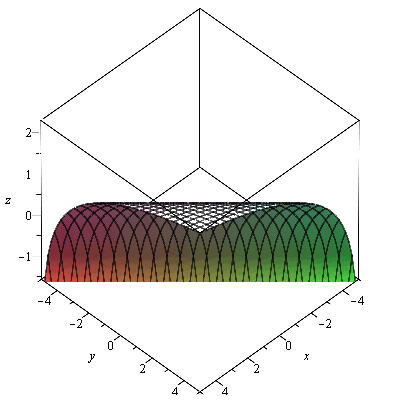
>	plot3d(f2, -5..5, -5..5, labels=[x, y, z]);

 

>

 

sqrt(1-x^2-y^2) 

funkce 

>	f3:=(x,y)->sqrt(1-x^2-y^2);

 

(3.1)

 

definiční obor 

>	inequal( {1-x^2-y^2>=0}, x=-2..2, y=-2..2, color=red);

 

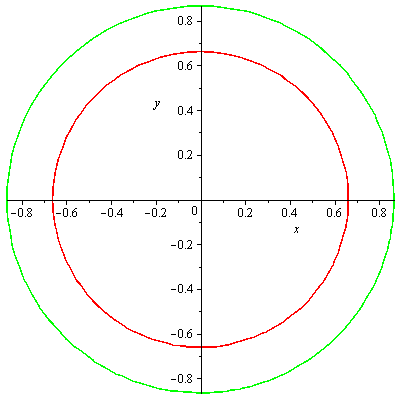
vrstevnice 

>	implicitplot([1-x^2-y^2=0.75^2,1-x^2-y^2=0.5^2], x=-3..3, y=-3..3,gridrefine = 2, color=[red,green]);

 

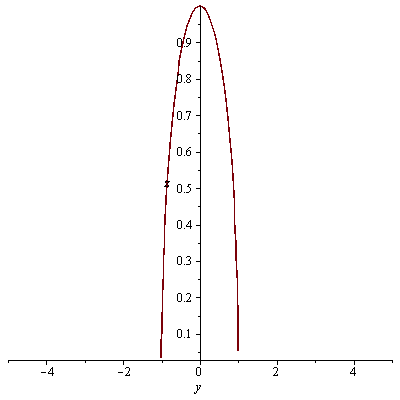
průsečnice s rovinami x=0 a y=0 

>	plot(f3(0,y),y=-5..5, labels=[y, z]); plot(f3(x,0),x=-5..5, labels=[x, z]);

 

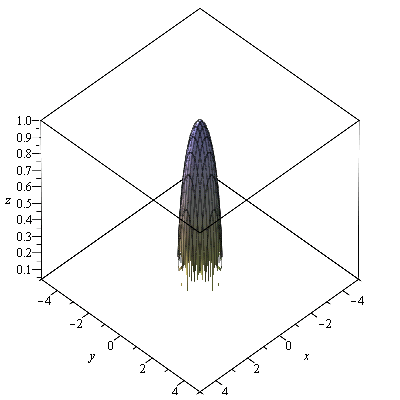
graf 

>	plot3d(f3, -5..5, -5..5,numpoints=10^5, labels=[x, y, z]);

 

>

 

|x|+|y| 

funkce 

>	f4:=(x,y)->abs(x)+abs(y);

 

(4.1)

 

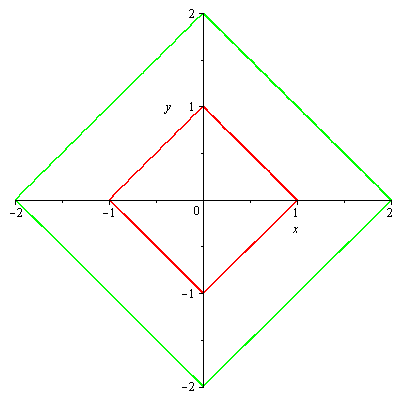
vrstevnice 

>	implicitplot([f4(x,y)=1,f4(x,y)=2], x=-3..3, y=-3..3,gridrefine = 2, color=[red,green]);

 

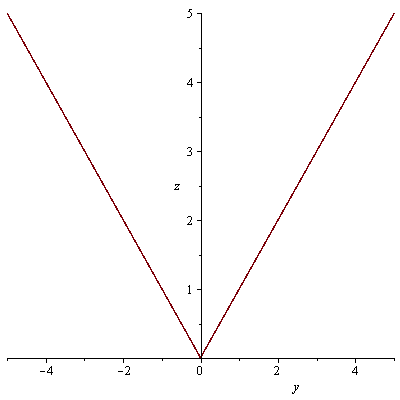
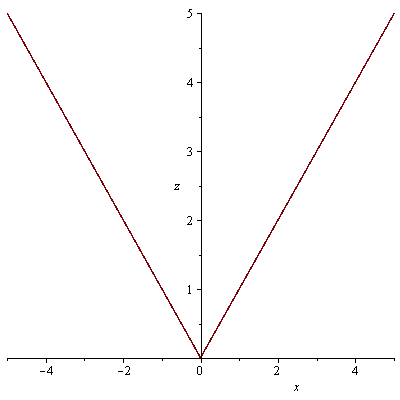
průsečnice s rovinami x=0 a y=0 

>	plot(f4(0,y),y=-5..5, labels=[y, z]); plot(f4(x,0),x=-5..5, labels=[x, z]);

 

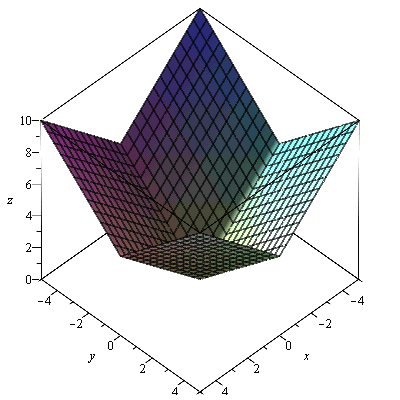
graf 

>	plot3d(f4, -5..5, -5..5, labels=[x, y, z]);

 

>

 

sqrt(x^2+y^2) 

funkce 

>	f5:=(x,y)->sqrt(x^2+y^2);

 

(5.1)

 

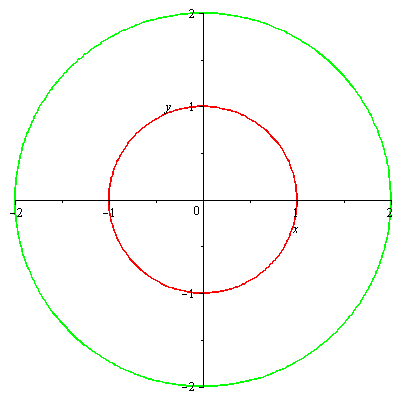
vrstevnice 

>	implicitplot([f5(x,y)=1,f5(x,y)=2], x=-3..3, y=-3..3,gridrefine = 2, color=[red,green]);

 

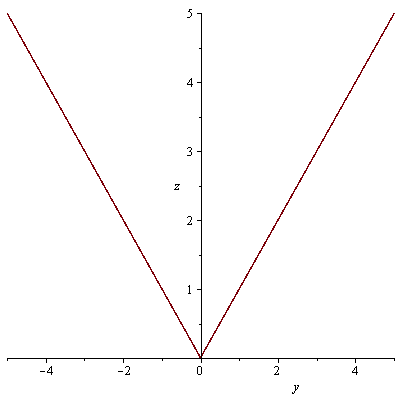
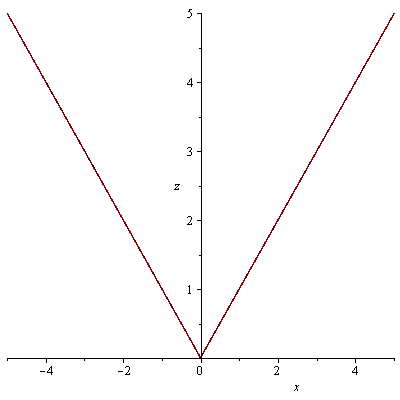
průsečnice s rovinami x=0 a y=0 

>	plot(f5(0,y),y=-5..5, labels=[y, z]); plot(f5(x,0),x=-5..5, labels=[x, z]);

 

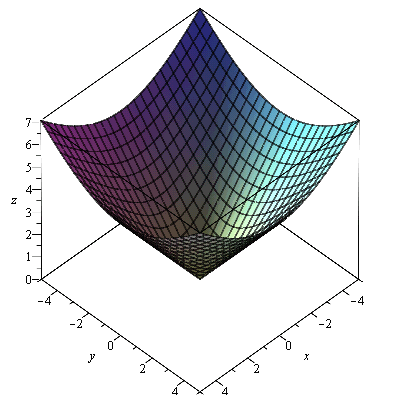
graf 

>	plot3d(f5, -5..5, -5..5, labels=[x, y, z]);

 

>

 

x^2+y^2 

funkce 

>	f6:=(x,y)->x^2+y^2;

 

(6.1)

 

vrstevnice 

>	implicitplot([f6(x,y)=1,f6(x,y)=2], x=-3..3, y=-3..3,gridrefine = 2, color=[red,green]);

 

průsečnice s rovinami x=0 a y=0 

>	plot(f6(0,y),y=-5..5, labels=[y, z]); plot(f6(x,0),x=-5..5, labels=[x, z]);

 

graf 

>	plot3d(f6, -5..5, -5..5, labels=[x, y, z]);

 

>

 

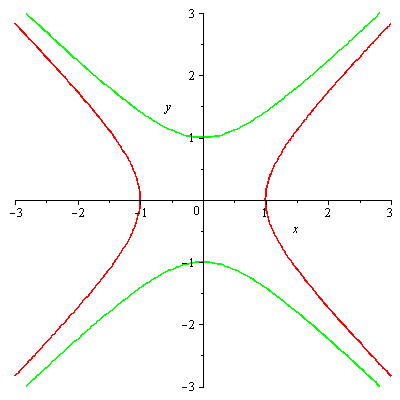
x^2-y^2 

funkce 

>	f7:=(x,y)->x^2-y^2;

 

(7.1)

 

vrstevnice 

>	implicitplot([f7(x,y)=1,f7(x,y)=-1], x=-3..3, y=-3..3,gridrefine = 2, color=[red,green]);

 

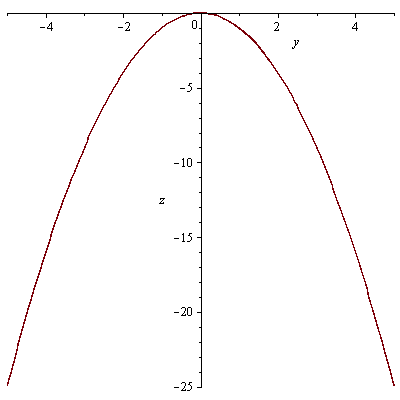
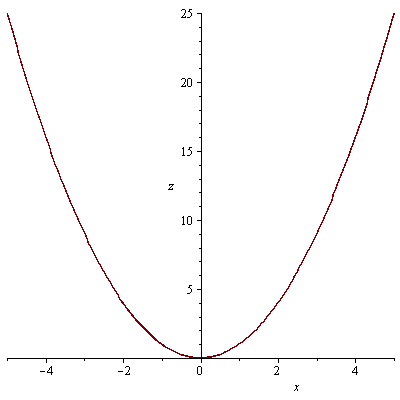
průsečnice s rovinami x=0 a y=0 

>	plot(f7(0,y),y=-5..5, labels=[y, z]); plot(f7(x,0),x=-5..5, labels=[x, z]);

 

graf 

>	plot3d(f7, -5..5, -5..5, labels=[x, y, z]);

 

>

 

exp(x) 

funkce 

>	f8:=(x,y)->exp(x);

 

(8.1)

 

vrstevnice 

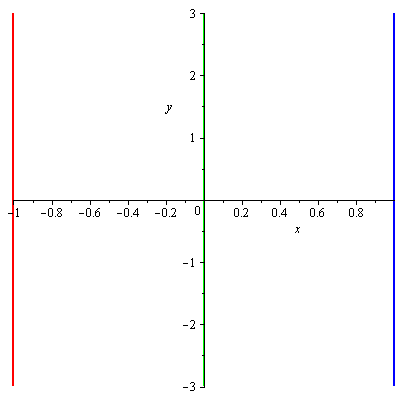
>	implicitplot([f8(x,y)=exp(-1),f8(x,y)=1,f8(x,y)=exp(1)], x=-3..3, y=-3..3,gridrefine = 2,color=[red,green,blue]);

 

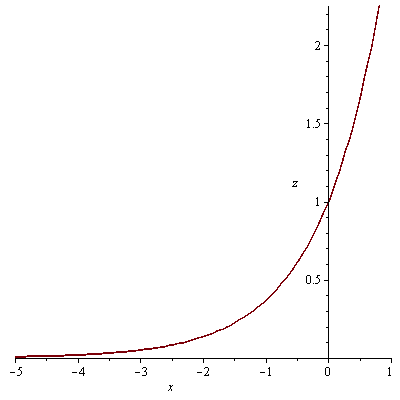
průsečnice s rovinami x=0 a y=0 

>	plot(f8(0,y),y=-5..5, labels=[y, z]); plot(f8(x,0),x=-5..5, labels=[x, z]);

 

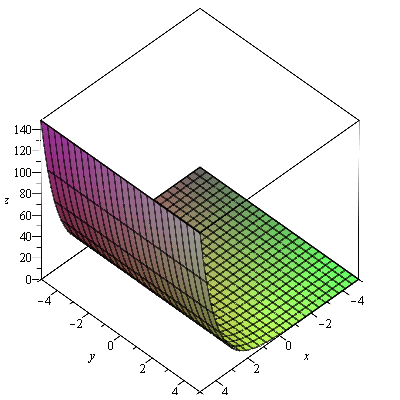
graf 

>	plot3d(f8, -5..5, -5..5, labels=[x, y, z]);

 

>

 

1-x-y 

funkce 

>	f9:=(x,y)->1-x-y;

 

(9.1)

 

vrstevnice 

>	implicitplot([f9(x,y)=-1,f9(x,y)=0,f9(x,y)=1,f9(x,y)=2], x=-3..3, y=-3..3, color=[red,green,orange,blue]);

 

průsečnice s rovinami x=0 a y=0 

>	plot(f9(0,y),y=-5..5, labels=[y, z]); plot(f9(x,0),x=-5..5, labels=[x, z]);

 

graf 

>	plot3d(f9, -5..5, -5..5, labels=[x, y, z]);

 

>

 

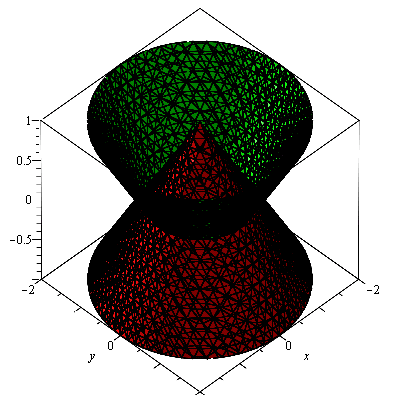
sqrt(1-sqrt(x^2+y^2)-z)+sqrt(1-sqrt(x^2+y^2)+z) 

>	implicitplot3d([1-sqrt(x^2+y^2)-z=0,1-sqrt(x^2+y^2)+z=0], x=-2..2, y=-2..2, z=-1..1, grid = [25,25,25], color=[red,green], labels=[x, y, z]);

 

Definičním oborem je "káča", prostor tvořený průnikem dvou kuželů.